Leyes de Kirchhoff parte 2

Por Ing. Hernán Hernández Jiménez

Recuerda que la primera Ley de Kirchhoff hace referencia a que en un circuito serie cerrado la corriente será la misma que circula en todo el circuito, sin embargo, para un circuito paralelo un nodo puede tener diferentes corrientes que entran y salen; por lo que para cada nodo los valores de corriente pueden variar.

Pasando entonces a la segunda ley, a esta se le conoce como Ley de tensiones y se aplica para circuitos serie y paralelo. Iniciemos el análisis en el más simple para esta ley: circuito paralelo.

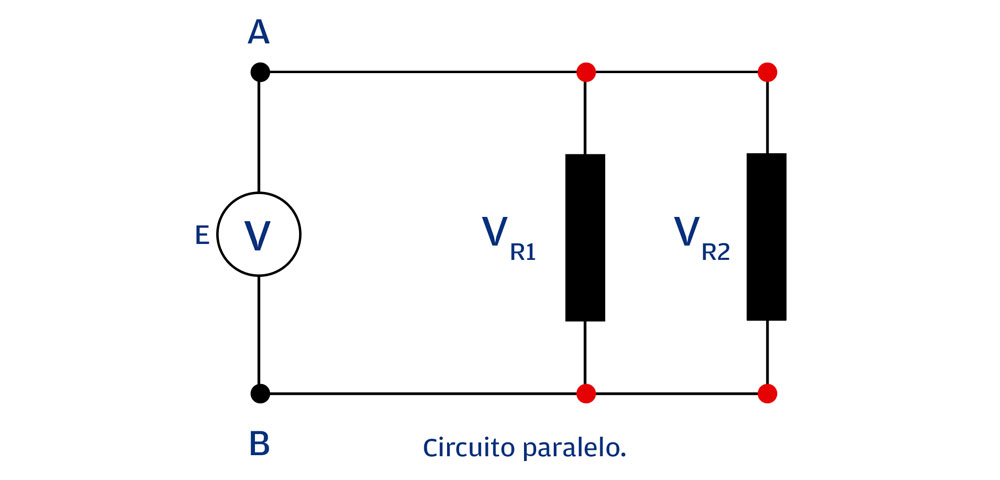
En un circuito paralelo donde se tiene una fuente de alimentación como en la imagen 1.

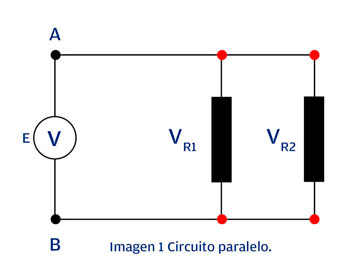
La tensión o diferencia de potencial entre los puntos A y B, es igual al valor de la tensión de la fuente. Para el caso de la R1 y R2 será el mismo valor, ya que la conexión se encuentra en paralelo a la fuente. Así es como se conectan los circuitos derivados en una instalación eléctrica para tener la misma tensión en las cargas. Para el caso del circuito paralelo lo podemos indicar de forma simple como:

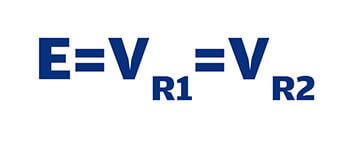
Las leyes de Kirchhoff complementadas con la de Ohm son herramientas de cálculo sumamente poderosas para incrementar las opciones de solución de circuitos eléctricos y electrónicos, los cuales son la base para entender el diseño de instalaciones eléctricas a cualquier escala.

La corriente se comportará de la forma en que se mencionó en la edición anterior. Veamos ahora como se comporta la tensión en un circuito serie como el de la imagen 2.

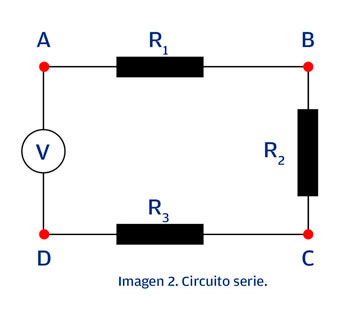
En este caso la tensión se distribuye entre las tres resistencias, por lo que la tensión entre los puntos A y B es diferente a la que existe entre B y C, asimismo la tensión entre C y D, a su vez, son diferentes a la tensión entre A y D que es la de la fuente. A este comportamiento, Kirchhoff lo representa como:

“La suma algebraica de las caídas de tensión es igual a cero”.
Veamos nuevamente el circuito colocando polaridad para cada caída de tensión y el flujo de la corriente en la imagen 3.

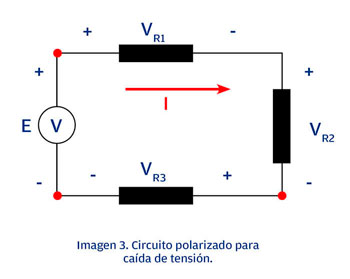
Tomamos el primer signo que encuentra el flujo de corriente para cada elemento e igualamos a cero:

Hecho esto, podemos pasar a la tensión E del otro lado del signo igual para tener todo con signo positivo:

Con lo anterior, ya tenemos descrita la segunda ley y podríamos determinar cualquiera de las tensiones.

Las leyes de Kirchhoff complementadas con la de Ohm son herramientas de cálculo sumamente poderosas para incrementar las opciones de solución de circuitos eléctricos y electrónicos, los cuales son la base para entender el diseño de instalaciones eléctricas a cualquier escala. Adicional a estas leyes se tienen los métodos de reducción de circuitos que consisten en obtener las resistencias equivalentes a fin de obtener la resistencia total. Estos métodos son sencillos y se aplican de forma puntal, dependiendo si el circuito a analizar es serie o paralelo.

Para un circuito serie el método de reducción consiste en sumar lo valores de las resistencias y obtener la resistencia total. Veamos el circuito de la imagen 4 con tres resistencias.

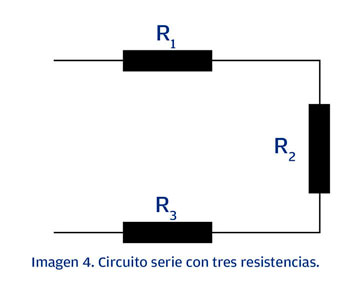
De las cuales R1= 15 Ω, R2= 5 Ω, R3= 10 Ω
Dado que es un circuito serie, sumamos todos lo valores por lo que R total=15+5+10=30Ω y el circuito se reduce a una resistencia total o equivalente (eq). Ver imagen 5.

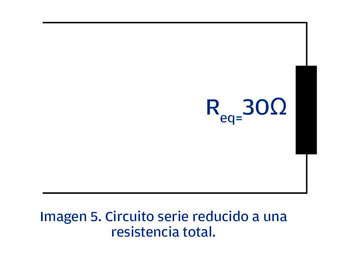
Para el circuito paralelo, el método de reducción se puede realizar de dos formas:
1. Aplicando de forma seccionada cada dos resistencias la siguiente ecuación:

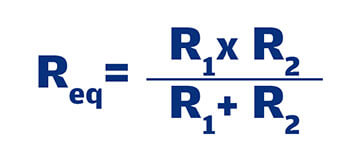
Cuando se tienen más de dos resistencias se deberá trabajar primero con dos para obtener la primera resistencia equivalente y posteriormente el paralelo con las siguientes.

2. Aplicando la siguiente ecuación:

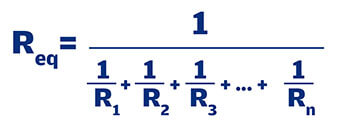
Esta es la más recomendable para cuando hay más de dos resistencias. Hasta aquí dejaremos lo correspondiente a las leyes de Kirchhoff.